Szögfüggvények

Info

Az animáción láthatod a szinusz és a koszinusz trigonometrikus függvények kapcsolatát az egységkörrel.

Az animáció két fő részből áll:

1. Egységkör és a rajta mozgó pontok:

   • A kör középpontja az origó ($0,0$), sugara 1 egység.
   • A körív mozgó fehér pontja az aktuális szöget jelöli ($\alpha$).
   • A narancssárga pont az $x$ tengelyen az aktuális szög koszinusz értéket mutatja, vagyis $x=\cos (\alpha )$.
   • A piros pont az $y$ tengelyen az aktuális szög szinusz értéket adja, vagyis $y=\sin (\alpha )$.

2. Grafikon:

   • $\alpha$ szög értékének változásával a függvényértékek változását lehet nyomonkövetni. Így látható a trigonometrikus függvények periodikus természete.

I. Bevezetés#

A trigonometria a matematika azon ága, amely a szögek és az ezekhez kapcsolódó mennyiségek – például oldalak, magasságok és szögfüggvények – vizsgálatával foglalkozik. Kulcsszerepet játszik a geometria, a fizika, a mérnöki tudományok, a csillagászat, valamint a technológia számos területén.

A trigonometria eszköztára lehetővé teszi, hogy meghatározzuk:

• háromszögek hiányzó oldalait vagy szögeit,
• az égitestek pozícióját,
• a hullámmozgásokat, rezgéseket,
• és sok más gyakorlati jelenséget.

Ebben a fejezetben megismerkedünk a szögfüggvények alapfogalmaival, azok geometriai értelmezésével és gyakorlati alkalmazásaival. Külön figyelmet szentelünk az egységkör szerepének, valamint szemléltetjük, hogyan változnak a szinusz és koszinusz értékek az egységkör mentén.

II. A Szögfüggvények Definíciója#

A szögfüggvények (például a szinusz, koszinusz, tangens) a derékszögű háromszögek szögei és oldalai közötti arányokat írják le. Ezek az arányok lehetővé teszik:

• a háromszög ismeretlen oldalainak kiszámítását,
• a szögek meghatározását,
• és a háromszögek tulajdonságainak elemzését.

A szögfüggvények nemcsak a síkgeometriában, hanem a körmozgás, a rezgéselmélet, a távolságmérés és a földrajzi helymeghatározás területén is alapvető fontosságúak.

Az alábbi ábra egy tipikus derékszögű háromszöget ábrázol, amelyen a szögeket és az oldalak neveit a matematikában szokásos módon tüntettük fel.

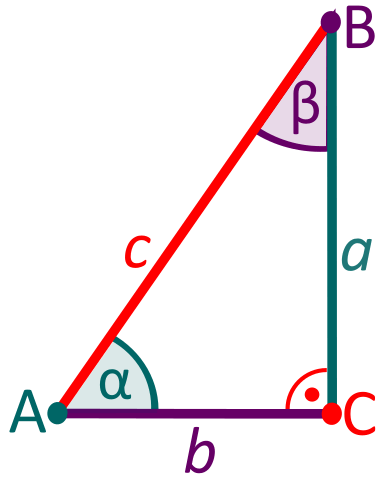
A $\theta$ jelölés jelentheti az $\alpha$ és a $\beta$ szögeket. Az alábbiakban a három alapvető szögfüggvényt mutatjuk be:

Szinusz ($\sin$)

• Definíció: A szöggel szembeni oldalnak és az átfogónak az aránya.
• Képlet:
  $$\sin (\theta )=\frac{\text{szo¨ggel szembeni oldal}}{\text{aˊtfogoˊ}}$$
• Példa:
  $$\sin (\alpha )(ejtsd:szinusz-alfa)=\frac{a}{c}$$

Koszinusz ($\cos$)

• Definíció: A szög melletti oldalának és az átfogónak az aránya.
• Képlet:
  $$\cos (\theta )=\frac{\text{szo¨g melletti oldal}}{\text{aˊtfogoˊ}}$$
• Példa:
  $$\cos (\alpha )(ejtsd:koszinusz-alfa)=\frac{b}{c}$$

Tangens ($\tan$)

• Definíció: A szöggel szembeni oldalának és a melletti oldalának az aránya.
• Képlet:
  $$\tan (\theta )=\frac{\text{szo¨ggel szembeni oldal}}{\text{szo¨g melletti oldal}}$$
• Példa:
  $$\tan (\alpha )(ejtsd:tangens-alfa)=\frac{a}{b}$$

III. Egységkör#

Az egységkör fogalma#

Az egységkör egy olyan kör, amelynek sugara 1 egység, és a középpontja az origóban van, azaz a koordinátarendszer $(0,0)$ pontjában helyezkedik el. Az egységkör kulcsszerepet játszik a trigonometriai szögfüggvények definíciójában.

A kör mentén mozgó pont segítségével a következő szögfüggvényeket definiálhatjuk:

• az $x$-koordináta a koszinusz,
• az $y$-koordináta a szinusz értéket adja.

Ábra – Egységkör és szögfüggvények#

Szögfüggvények az egységkörben#

A szögfüggvényeket az egységkörön az origóból induló vektor és az $x$-tengely által bezárt szög alapján határozzuk meg. A vektor végpontja az egységkör egy pontja, és a szögfüggvények értékei ehhez a ponthoz kötődnek:

Szinusz:

Az egységkör pontjának $y$-koordinátája.

Koszinusz:

Az egységkör pontjának $x$-koordinátája.

Tangens:

Azaz a szinusz és koszinusz hányadosa, ha $x\ne 0$.

Példa Számítás#

$\alpha =45^{\circ }$ vagy $\frac{\pi }{4}$ radián esetén az egységkörön a szöghöz tartozó pont koordinátái:

Ez alapján:

• $\sin (45^{\circ })\approx 0,707$
• $\cos (45^{\circ })\approx 0,707$
• $\tan (45^{\circ })=\frac{0,707}{0,707}=1$

Ezek az értékek az egységkör megfelelő pontjából közvetlenül leolvashatók.

További észrevételek az egységkörrel kapcsolatban#

• Az egységkörön mozgó pont minden szög esetén egyértelműen meghatározza a szögfüggvények értékeit.
• A negatív szögek az óramutató járásával ellentétes irányban haladnak.
• A kör minden pontjához tartozik egy szög, és így minden valós számhoz hozzárendelhető egy szögfüggvény érték.

IV. Kapcsolatok és Alapvető Azonosságok#

A trigonometrikus szögfüggvények között szoros matematikai kapcsolatok állnak fenn. Ezek az azonosságok segítenek a szögfüggvények közötti átváltásokban, az ismeretlen értékek kiszámításában, valamint a trigonometrikus kifejezések egyszerűsítésében.

Warning

A helyes alkalmazásukhoz fontos érteni a szögek helyzetét az egységkörben és a különböző kvadránsok jellegzetességeit.

1. Pitagoraszi azonosság#

A legismertebb összefüggés a szinusz és a koszinusz között:

Ez az azonosság az egységkör geometriájából következik, ahol minden pont távolsága az origótól (azaz az $x^2+y^2$) mindig 1.

Példa:

Ha adott:

akkor a koszinusz számítása:

Info

Az előjel ($+$ vagy $-$) attól függ, melyik kvadránsban van az $\alpha$ szög:

• I. kvadráns: $\sin (\alpha )>0,\cos (\alpha )>0$
• II. kvadráns: $\sin (\alpha )>0,\cos (\alpha )<0$
• III. kvadráns: $\sin (\alpha )<0,\cos (\alpha )<0$
• IV. kvadráns: $\sin (\alpha )<0,\cos (\alpha )>0$

2. Tangens kifejezése szinusz és koszinusz alapján#

A tangens az alábbi arányként is megadható:

Ez közvetlenül következik a definícióból, mivel az egységkörön a tangens egyenesen a szinusz és koszinusz koordináták hányadosa.

Példa:

Ha:

akkor:

3. Kiegészítő szögek azonosságai#

A trigonometrikus függvények kiegészítő szögekkel való viszonya a következő szabályokat adja:

Ezek a szabályok azt mutatják meg, hogyan lehet az egyik szögfüggvény értékét egy másik szög kifejezésével megadni. Ezek az azonosságok különösen hasznosak derékszögű háromszögeknél és trigonometrikus egyenletek átalakításánál.

4. Tangens és kotangens kapcsolat#

A tangens és a kotangens is kapcsolódik egymáshoz, valamint a szinusz és koszinusz négyzetösszegéhez:

V. Szögfüggvények Alkalmazásai#

A szögfüggvények nem csupán elméleti matematikai fogalmak, hanem számos tudományos és gyakorlati területen alkalmazhatók. A szög, a szögfüggvények és a trigonometria összekapcsolja a geometriát a fizikával, a csillagászattal, az építészettel és a technológiával.

A. Derékszögű háromszög számításai#

A trigonometria legismertebb alkalmazása a derékszögű háromszög oldalainak és szögeinek kiszámításában rejlik. Az alábbi képletek alkalmazhatók:

A. Ha ismert egy hegyesszög és a szemben lévő befogó:

B. Ha ismert egy hegyesszög és a mellette lévő befogó:

C. Ha két befogó arányát ismerjük:

Tip

Példa: Egy létra 5 m hosszú, és a falnak 60°-os szögben támaszkodik. Milyen magasra ér fel a falon?

$$\sin (60^{\circ })\approx 0.866\Rightarrow \text{magassaˊg}=5\cdot 0.866=4.33\text{m}$$

B. Csillagászat és földrajzi helymeghatározás#

A csillagászatban a szögfüggvényeket használják:

• A csillagok látszólagos magasságának meghatározására (ld. 7. fejezet).
• Az égitestek deklinációjának, óraszögének és horizont feletti szögének számítására.
• A parallaxis módszerben a közeli csillagok távolságának meghatározásához.

Tip

Érdekesség: A Föld tengelyferdesége miatt a Nap szögmagassága a nap folyamán változik. A szinusz és koszinusz segítségével modellezhetjük a nappalok hosszát és a Nap járását.

C. Navigáció és tájolás#

A trigonometria évszázadok óta alapja a hajózási és légi navigációnak:

• Az irányvonalak (pl. kompensált iránytű) szögei alapján számítják ki a megtett távolságot.
• A radarhullámok szögéből meghatározható az objektum helyzete.
• A GPS rendszerek háromszögeléssel határozzák meg a pontos földrajzi pozíciót.

D. Építészet és műszaki tervezés#

A szögek és arányok használata minden tervezési folyamatban kulcsfontosságú:

• Tetőszerkezetek dőlésszöge, ablakok beesési szögei.
• Hidak, rámpák, lépcsők tervezése szög- és távolságszámítás alapján.
• Fény beesési szögének optimalizálása (pl. napkollektorok).

Tip

Példa: Egy napelemet úgy kell elhelyezni, hogy a napsugarak a legmeredekebb szögben érjék. Ezt az évszakos napállás szögével és a földrajzi szélességgel számolják ki.

E. Fizika és hullámmozgás#

A trigonometria segít leírni a hullámjelenségeket:

A harmonikus rezgőmozgás egy szinuszfüggvénnyel írható le:

ahol: $A$ az amplitúdó, $\omega$ a körfrekvencia, $\phi$ a fáziseltolás.

Az elektromágneses hullámok leírásához szintén szinusz-koszinusz függvényeket alkalmazunk.

F. Informatika és jelfeldolgozás#

• A digitális jelfeldolgozás (DSP) egyik alapköve a Fourier-analízis, amely trigonometrikus sorfejtésen alapul.
• Kép- és hangmanipuláció során a jelrendszerek szinuszos komponensek szerint bonthatók fel.
• A grafikában és animációban szögfüggvények segítségével hoznak létre forgásokat, lengéseket, hullámszerű mozgást.

Info

A szögfüggvények tehát sokkal többek puszta képleteknél: a világ megértésének eszközei. Alkalmazásuk segít modellezni, kiszámítani és optimalizálni folyamatokat – legyen szó csillagokról, napelemekről vagy mobiltelefonokról.

VI. A Szögfüggvények Grafikonjai#

A trigonometriai függvények – szinusz, koszinusz, tangens – nemcsak szögekhez rendelnek értékeket, hanem folytonos matematikai függvényekként is értelmezhetők. Ezek grafikonjai segítségével jobban megérthetjük viselkedésüket, például:

• hol veszik fel a maximális vagy minimális értéküket,
• hol nullák az értékeik,
• milyen periódusúak,
• és hogyan változnak különböző szögtartományokban.

A függvényeket az $\alpha$ szöggel jelöljük, amelynek értéke radiánban értendő (de gyakran fokban is használatos szemléltetés céljából).

1. Szinuszfüggvény#

A szinuszfüggvény a szöghöz tartozó egységkörbeli pont $y$-koordinátáját adja meg.

Tulajdonságai:

• Periódus: $2\pi$ – a függvény minden $2\pi$ szög után ismétlődik.
• Értékkészlet: $[-1,1]$
• Zérushelyek: $\alpha =0,\pi ,2\pi ,\dots$
• Maximum: $\sin (\alpha )=1$, pl. $\alpha =\frac{\pi }{2}$
• Minimum: $\sin (\alpha )=-1$, pl. $\alpha =\frac{3\pi }{2}$
• Szimmetria: páratlan függvény, azaz $\sin (-\alpha )=-\sin (\alpha )$

Grafikon:

2. Koszinuszfüggvény#

A koszinuszfüggvény a szöghöz tartozó egységkörbeli pont $x$-koordinátáját adja meg.

Tulajdonságai:

• Periódus: $2\pi$
• Értékkészlet: $[-1,1]$
• Zérushelyek: $\alpha =\frac{\pi }{2},\frac{3\pi }{2},\dots$
• Maximum: $\cos (\alpha )=1$, pl. $\alpha =0$
• Minimum: $\cos (\alpha )=-1$, pl. $\alpha =\pi$
• Szimmetria: páros függvény, azaz $\cos (-\alpha )=\cos (\alpha )$

Grafikon:

3. Tangensfüggvény#

A tangensfüggvény a szög szinuszának és koszinuszának hányadosa:

Tulajdonságai:

• Periódus: $\pi$
• Értékkészlet: $(-\infty ,+\infty )$
• Zérushelyek: $\alpha =0,\pi ,2\pi ,\dots$
• Nincs maximum/minimum – a függvény értéke végtelenhez tart az aszimptoták közelében.
• Függőleges aszimptoták: ott, ahol $\cos (\alpha )=0$ (pl. $\alpha =\frac{\pi }{2},\frac{3\pi }{2}$)

Grafikon:

Összefoglaló táblázat#

Függvény	Periódus	Értékkészlet	Zérushelyek	Megjegyzés
$\sin (\alpha )$	$2\pi$	$[-1,1]$	$0,\pi ,2\pi ,\dots$	Hullám, páratlan függvény
$\cos (\alpha )$	$2\pi$	$[-1,1]$	$\frac{\pi }{2},\frac{3\pi }{2}$	Fáziseltolás, páros függvény
$\tan (\alpha )$	$\pi$	$(-\infty ,+\infty )$	$0,\pi ,2\pi ,\dots$	Aszimptotás, páratlan

Tip

Mindezek a függvények radiánban értelmezettek, de oktatási célból fokban is használhatók (pl. $\pi =180^{\circ }$). Radián és fok átváltás kalkulátor

VII. Inverz Szögfüggvények#

Az inverz szögfüggvények lehetővé teszik, hogy egy adott szögfüggvény-értékhez megtaláljuk a hozzátartozó szöget. Ez különösen fontos olyan problémákban, ahol az arányokat ismerjük, de a szöget keressük – például derékszögű háromszög szögeinek meghatározásánál, vagy szögek visszafejtésénél trigonometrikus egyenletekben.

Mi az inverz szögfüggvény?#

Egy függvény inverze a bemeneti és kimeneti értékek „felcserélését” jelenti. Az inverz szögfüggvények jelölése:

• $\arcsin (x)$ – az a szög, amelynek szinusza $x$
• $\arccos (x)$ – az a szög, amelynek koszinusza $x$
• $\arctan (x)$ – az a szög, amelynek tangense $x$

Inverz szinusz#

Definíció:

Tulajdonságai:

• Értelmezési tartomány: $x\in [-1,1]$
• Értékkészlet (szög): $\alpha \in \left[-\frac{\pi }{2},\frac{\pi }{2}\right]$
• Növekvő függvény, szimmetrikus az origóra.

Példa:

Grafikon:

Inverz koszinusz#

Definíció:

Tulajdonságai:

• Értelmezési tartomány: $x\in [-1,1]$
• Értékkészlet (szög): $\alpha \in [0,\pi ]$
• Csökkenő függvény.

Példa:

Grafikon:

Inverz tangens#

Definíció:

Tulajdonságai:

• Értelmezési tartomány: $x\in \mathbb{R}$
• Értékkészlet (szög): $\alpha \in \left(-\frac{\pi }{2},\frac{\pi }{2}\right)$
• Folyamatos, szigorúan növekvő függvény.

Példa:

Grafikon:

Áttekintő táblázat#

Függvény	Jelölés	Bemenet $x$	Kimenet (szög $\alpha$)	Példa
Inverz szinusz	$\arcsin (x)$	$[-1,1]$	$[-\frac{\pi }{2},\frac{\pi }{2}]$	$\arcsin (0.5)=30^{\circ }$
Inverz koszinusz	$\arccos (x)$	$[-1,1]$	$[0,\pi ]$	$\arccos (0.5)=60^{\circ }$
Inverz tangens	$\arctan (x)$	$(-\infty ,\infty )$	$(-\frac{\pi }{2},\frac{\pi }{2})$	$\arctan (1)=45^{\circ }$

Warning

Az inverz szögfüggvények csak az elsődleges megoldást adják vissza – azt, amely az értelmezési tartományon belül van. Azonban egy adott szögfüggvény-értékhez végtelen sok szög is tartozhat, hiszen a trigonometrikus függvények periodikusak.

Példa:

$$\sin (\alpha )=0.5\Rightarrow \alpha =30^{\circ }+360^{\circ }\cdot k\text{vagy }150^{\circ }+360^{\circ }\cdot k$$

Az $\arcsin (0.5)$ csak a $30^{\circ }$-ot adja vissza!

Alkalmazások#

• Derékszögű háromszögek szögeinek visszafejtése
• Trigonometrikus egyenletek megoldása
• Jelfeldolgozás, ahol egy adott szögfüggvény-értékhez a fázisszöget kell meghatározni
• Fizikai rendszerek visszafejtése (pl. rezgőmozgás szögfázisa)

Info

Az inverz szögfüggvények hidat képeznek a függvényértékek és a mögöttes szögek között. Használatuk elengedhetetlen, ha a szöget akarjuk meghatározni egy ismert arány vagy trigonometrikus érték alapján.

VIII. Csillagmagasság Számítása Trigonometriai Módszerekkel#

Fogalmak#

A csillagászati helymeghatározás egyik alapfogalma a csillagmagasság vagy horizont feletti magasság, amely azt mutatja meg, hogy egy adott csillag milyen szögmagasságban látszik a horizont felett. Ennek meghatározása fontos szerepet játszik az égbolt térképezésében, navigációban és a megfigyelések tervezésében. A számítás trigonometriai szögfüggvényeken alapul, és a földrajzi szélesség, valamint a csillag deklinációja ismeretében végezhető el.

• 🌄 Horizont feletti magasság (altitude / eleváció) egy szög, amely azt mutatja meg, hogy egy égitest milyen magasan van a horizont fölött a megfigyelő szemszögéből nézve. A horizont feletti magasság valós, megfigyelhető szög, amit akár szextánssal is mérhetsz.
  • Jelölés: $h$
  • Mértékegység: fok (°)
  • Képlet:
    $$\sin (h)=\sin (\phi )\cdot \sin (\delta )+\cos (\phi )\cdot \cos (\delta )\cdot \cos (t)$$
    ahol:
    • $\phi$ a megfigyelő földrajzi szélessége,
    • $\delta$ a csillag deklinációja.
    • $t$ = óraszög. /Az óraszög annak a szögnek felel meg, amelyet a csillag helyi délkörhöz (meridiánhoz) képest zár be az égi egyenlítő mentén, az idő múlásával nyugat felé haladva./
  • Tartomány: $0^{\circ }$ (horizont) – $90^{\circ }$ (zenit, azaz fej fölött)
  • Felhasználás:
    • Égbolt-térképek,
    • Navigáció,
    • Távcső beállítása,
    • Csillagászati megfigyelések
• Földrajzi szélesség azt jelenti, hogy a Föld felszínén a megfigyelő milyen távolságra van az Egyenlítőtől és melyik irányban.
• Deklináció azt jelenti, hogy az égi egyenlítőtől az objektum hol helyezkedik el az égi koordináta-rendszerben.
• 🌐 Vetületi magasság, mely nem szög, hanem egy távolság, amelyet általában a Föld középpontjából indított geometriai modell alapján számítunk ki. Ez azt fejezi ki, hogy egy csillag „milyen magasan” lenne a Föld görbületéhez képest, ha a megfigyelő pont vetületében mérnénk.
  • Jelölés: $H$
  • Mértékegység: km (vagy m)
  • Képlet:
    $$H=R\cdot \cos (\phi -\delta )$$
    ahol:
    • $R$ a Föld sugara (pl. 6371 km),
    • $\phi$ a megfigyelő földrajzi szélessége,
    • $\delta$ a csillag deklinációja.
  • Felhasználás:
    • Trigonometriai számításokban, amikor a csillag vetületi helyzetét vizsgáljuk,
    • Modellezéshez, amikor a Föld geometriáját vesszük figyelembe,
    • Navigációs algoritmusokban, optikai rendszerek előzetes tájolásához.

Példa a Szíriusz csillaggal#

Ebben a példában kiszámítjuk a Szíriusz csillag vetületi magasságát és horizont feletti magasságát trigonometriai módszerrel.

Kiinduló adatok:

• Megfigyelő földrajzi szélessége: $\phi =45^{\circ }$
• Szíriusz deklinációja: $\delta =-16,7^{\circ }$
• Föld sugara: $R=6371\text{km}$

I. Vetületi magasság#

Képlet:

A vetületi magasság szögének meghatározásához a következő összefüggést használjuk:

Ez a képlet feltételezi, hogy a csillag lokális delelésben van, vagyis a megfigyelő meridiánján látszik ($t=0^{\circ }$).

Lépésenkénti levezetés:

1. Szög kiszámítása:

Info

Ez a szög azt jelenti, hogy a csillag (Szíriusz) milyen szögben „távolodik el” az égi egyenlítőtől a megfigyelő földrajzi szélessége alapján – de nem maga a csillagmagasság.

2. Koszinusz érték:

3. Magasság számítása:

Eredmény:

A Szíriusz horizont feletti vetületi magassága körülbelül 3088 km.

Info

Valódi távolság ≠ Vetületi magasság

• Valódi távolság: A Szíriusz tényleges távolsága a Földtől körülbelül 8,6 fényév, ami kb. 81,3 billió kilométer. Ezt a távolságot nem trigonometriai úton, hanem asztrometriai mérésekkel határozzák meg, például a parallaxis módszerével.
• Vetületi magasság: Az itt számított 3088 km kizárólag a megfigyelő pozíciójára és a Föld geometriájára vonatkozik, és a csillagászati helyzet lokális értelmezését szolgálja.

II. Horizont feletti magasságának kiszámítása#

A horizont feletti magasság – más néven csillagmagasság – az alábbi trigonometriai képlettel számítható:

Ahol:

• $h$ = horizont feletti magasság (fokban),
• $\phi$ = megfigyelő földrajzi szélessége,
• $\delta$ = csillag deklinációja,
• $t$ = óraszög (a példában $t=0^{\circ }$).

Behelyettesítve:

• $\phi =45^{\circ }$
• $\delta =-16,7^{\circ }$
• $t=0^{\circ }$

Magasságszög meghatározása:

Eredmény:

A Szíriusz horizont feletti magassága a megfigyelő 45°-os földrajzi szélességéről nézve, amikor a csillag delel, körülbelül:

28,3°

Ez a ténylegesen látható szög, amely alatt a Szíriusz az égen megjelenik a horizont fölött.

Eredmények összefoglaló táblázata#

Mennyiség	Érték
Számított szög	$61,7^{\circ }$
Koszinusz értéke	$0,4848$
Vetületi magasság	$\approx 3088$ km
Valódi távolság	$\approx 81,3$ billió km
Horizont feletti magasság	$28,3°$

Kapcsolódó tartalmak#

1. Szögfüggvény kalkulátor Számolja ki gyorsan a szinusz, koszinusz, tangens és fordított függvények értékeit precíz eredményekkel.
2. Derékszögű háromszög kalkulátor Derékszögű háromszög kalkulátor, mellyel kiszámíthatja a háromszög kerületét, területét és szögeit különböző bemeneti adatpárokból.

Gyakran Ismételt Kérdések (FAQ)#

Miért hívják "trigonometria"-nak ezt a matematikai ágat?

A "trigonometria" szó a görög trigonon (háromszög) és metron (mérés) szavakból származik. Eredetileg a háromszögek oldalainak és szögeinek mérésével foglalkozott, majd később kibővült az egységkör és periodikus függvények vizsgálatára.

Mi az egységkör, és miért fontos a trigonometria szempontjából?

Az egységkör egy olyan kör, amelynek sugara 1, középpontja pedig az origó ($0,0$). Az egységkör azért fontos, mert a szögfüggvényeket (szinusz, koszinusz, tangens) az egységkör pontjainak koordinátáival definiáljuk: $\sin (\theta )$ az $y$-, míg $\cos (\theta )$ az $x$-koordináta.

Hogyan kapcsolódik a tangens az egységkörhöz?

Az egységkörben a tangens értéke a szöghöz tartozó pont $y$- és $x$-koordinátájának aránya:

$$\tan (\theta )=\frac{\sin (\theta )}{\cos (\theta )}.$$

Geometriailag a tangens a kör érintőjének metszéspontjához tartozó koordináta.

Mit jelent a "szinusz" szó?

A "szinusz" a latin sinus szóból ered, ami öblöt jelent. Eredetileg egy arab matematikai szöveg félkör alakú ívét jelölte, majd a latin fordítók sinus-ként említették. Innen terjedt el a mai matematikai értelemben.

Mi a különbség a radián és a fok között?

A radián és a fok szögmérési egységek. Egy teljes kör 360 fok vagy $2\pi$ radián. Egy radián a körív hosszával ($r$) arányos:

$$1\text{radiaˊn}=\frac{180^{\circ }}{\pi }.$$

Hogyan számítjuk ki egy derékszögű háromszög területét szögfüggvényekkel?

Ha ismerjük egy derékszögű háromszög két oldalát ($a$ és $b$), a terület kiszámítható:

$$T=\frac{1}{2}\cdot a\cdot b.$$

Ha az egyik szög ($\alpha$) és egy oldal ismert, a terület:

$$T=\frac{1}{2}\cdot a\cdot b\cdot \sin (\alpha ).$$

Érdekesség: Hogyan kapcsolódik a trigonometria a navigációhoz?

A trigonometria az ókor óta alapvető szerepet játszik a navigációban. A szögfüggvények segítségével a tengerészek kiszámíthatták a Nap és a csillagok magasságát, ezáltal meghatározva pozíciójukat a nyílt tengeren.